This is a very important step, and I would like to explain in details what it really means. As a physicist, I have to do that.

De facto it means that we accept the  fact that price and time can be considered as a kind of space, a kind of time-price unity. This is not a simple physical process when the price is changing inside a time domain (like air temperature or pressure changes in time, and we simply record these changes). No, it is more complicated as we delegate to the price the quality of space . Price does not changes in regards to the time; it changes due to the involvement of a human being (a trader) who walks in this time-price Universe, though in regards to the time it is a one way road.

 Why is it so important to accept (or not accept) this fact? Simply because the acceptance or not acceptance of this fact gives us an ability to apply or not apply the mathematics. Usually the academic science prefers not working with the price directly, using instead some normalized values like oscillators or percentage of daily gains, etc. It sets the price in a Procrustean bed of normalized/uniformed values, as an inevitable result of this procedure is that we can forecast timing but not price values. Possibly for the next step we have to loose our academic virginity (but not the scientific common sense).

 Some analogy can be found in the evolution of science. More than 100 years ago Herman Minkowski  introduced four-dimensional spacetime manifold  that incorporates space and time in one coordinate system. This simple formalism helped Albert Einstein to develop famous Einstein field equations. General theory of relativity shows how gravitation affects our four dimensional spacetime Universe making it curved. To build the building of new post-Newtonian physics, we have to interpolate our Universe as four dimensional spacetime, we cannot separate this unity.

Now in 21 century this fact is very obvious for everybody. For example, look at what we can read in Wikipedia:

"Astronomers in the US have measured the distance of the farthest known galaxy, finding that its light took 13.1 billion years to reach Earth – which means the light was emitted just 700 million years after the Big Bang. Although the galaxy is much smaller than the Milky Way, it is forming stars at a much faster...; Oct 23, 2013" 

You easily understand that this galaxy is located 13.1 billion years from Earth - this is space distance. At the same time, we understand that we are looking at OUR OWN history 13.1 billion years ago, 700 million years after Big Bang - this is time distance.

Why I have to use so many words about that? You see, if we accept the fact that price has a quality of space, we may try to apply another model. As a simple example, we can calculate some formula that describes some market move in regards to price; instead of creating a function like Sinus(time), we could use Sinus(price). Right now, in all 600+ K lines of Timing Solution code, you will not find this formula, as we cannot compare oranges (price) and apples (angles).

Second step: price time ratio - information speed

Now we have to set up the ratio between price and time domains. In example above we used a scale where 1 point of S&P500 corresponds to 1 degree of the Sun movement. For Dow Jones it would be better to use another ratio: 10 points of DJII movement corresponds to 1 degree of Sun movement. Back to Minkowski spacetime manifold, the role of scaling coefficient between time and space plays the speed of light. And I would like to clarify one nuance here (this is a quote from Wikipedia):

"According to special relativity, c is the maximum speed at which all matter and hence information in the universe can travel. It is the speed at which all massless particles ...."   You see, we speak more about information than speed itself, how fast the information can be delivered. BTW, pay attention: they speak about massless particles because mass becomes infinity around the speed of light.

Ok, almost done. The last question is about metric formula, how to calculate the distance between two points in our new pricetime Universe. For example above, we used this formula, the distance between two points 1 and 2 calculates this way:

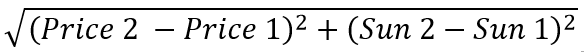
The time here is measured in the Sun movement units, so (Sun 2 - Sun 1) means the increment in the Sun position within this period. For example, within one year the Sun makes one full cycle through Ecliptic, i.e. 360 degrees; for ten years it is 3600 degrees, etc.

For Dow it is better to scale the price as 1 degree of the Sun movement corresponds to 10 points of Dow change, so the distance between two points 1 and 2 is calculated this way:

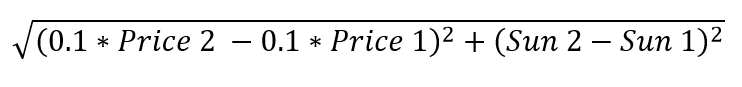
Pay attention, the distance between points in our pricetime Universe is calculated in degrees of the Sun (or any other planet's) movement. You will see later why this metrics is more convenient. And last note a-la physicist: the signature of this metrics is (+,+) which means that we consider price and time as similar dimensions, like we will work with two kinds of time, two dimensions of time. In the next section I will explain why this is important.

Equidistant circle

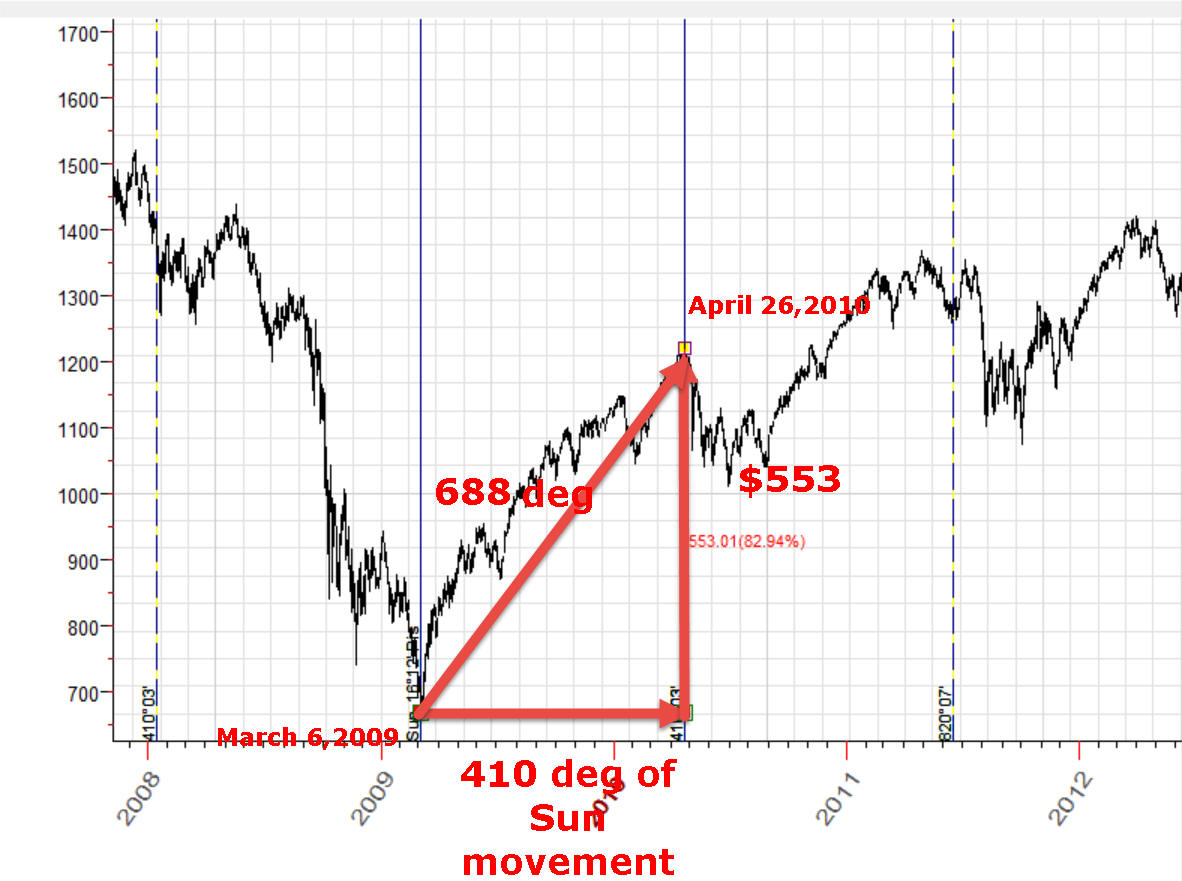
Now, let 's go back to our first chart. We have calculated there the distance between two turning points 1 and 2; it is 688 degrees of the Sun movement. You can plot all points with the same 688 degrees distance from initial point 1:

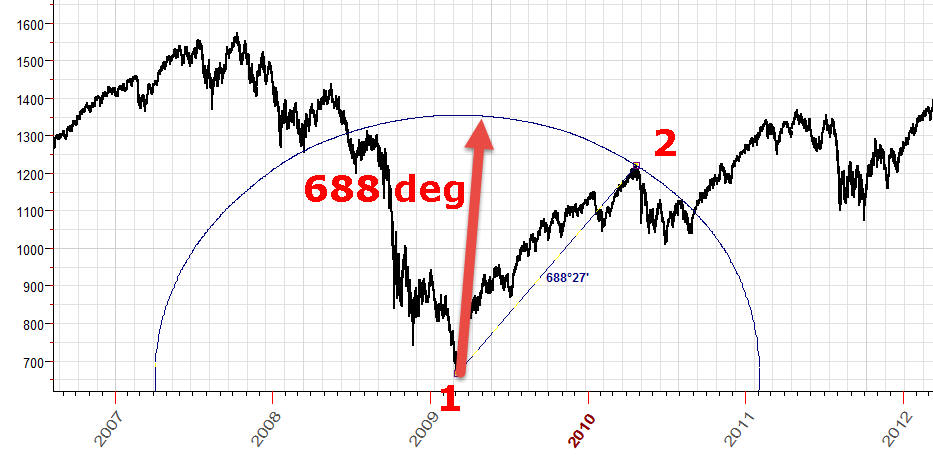
Regarding the metric signature: if we assume that the signature for our pricetime Universe is (+1,-1), i.e. price is a kind of space, the equidistant curve will look this way:

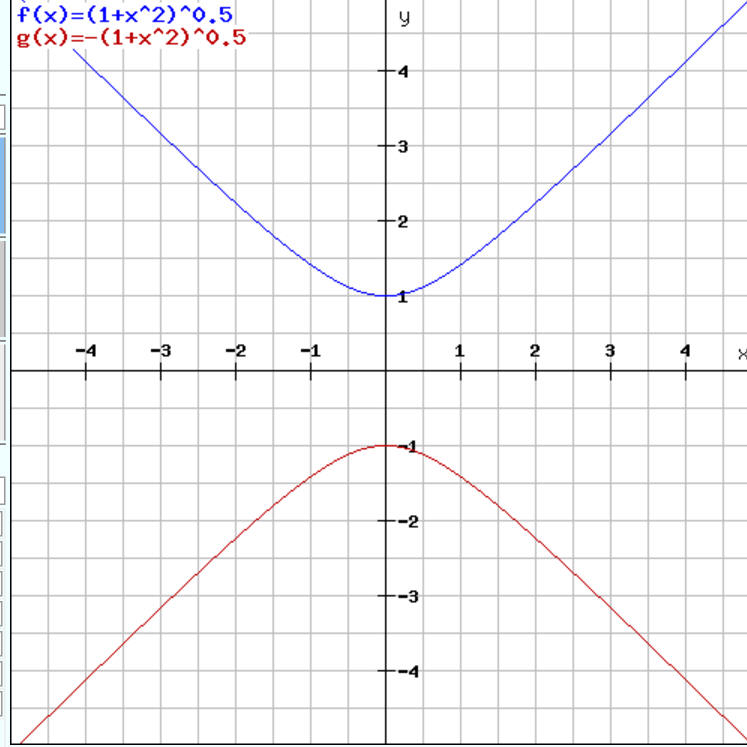
It does not look logical to me, so I have decided to use (+1,+1) pricetime space with ellipses provided by this approach (ellipses - because this is a widely used figure of technical analysis).

Scaling

In this example we use scaling ratio 1degree of the Sun movement=$1 of S&P500 movement. Let's modify this ratio a little and set it to 1 degree=$0.934419. This is the chart we get:

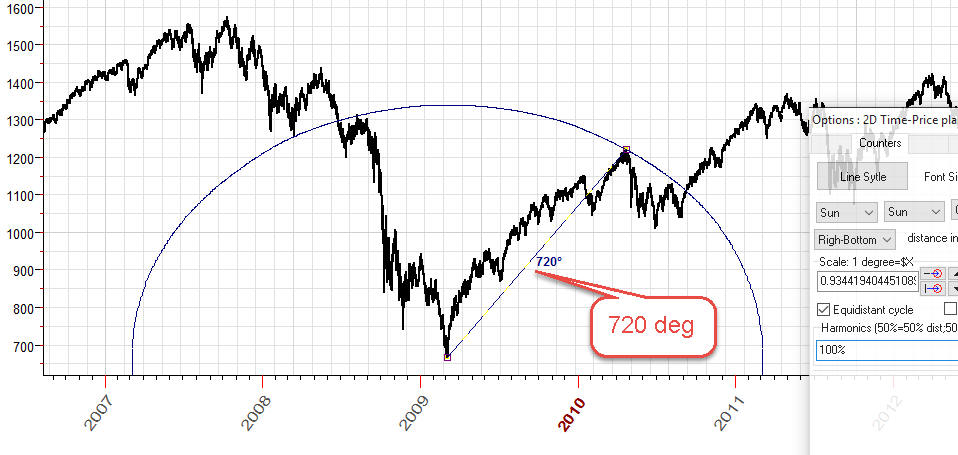
The distance between these turning points is 720 degrees i.e. exactly two full cycles. Accordingly the equidistant circle is modified a bit, now it hits slightly different points of the price chart.

Harmonics

The same manner we can draw equidistant circles based on 360, 1080 (=3x360), 1440 (=4x360) degress. They look pretty much the same as standard concentric ellipses charting tools:

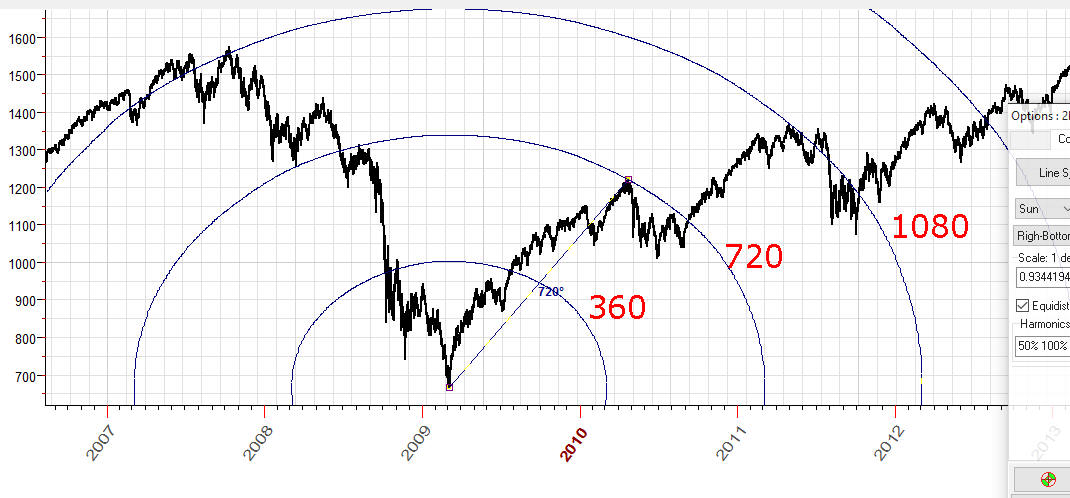
We can try to analyze these equidistant ellipses as some kind of information waves. Two important turning points are explained by two full waves (720 degrees). Ok, let's try also 360, 1080 etc. degrees ellipses, may be these ellipses bring some new information for us ... just an idea.

Basic hypothesis

 As a basic hypothesis, we can use this: for a properly scaled chart, the distance between important turning points should form "good" angles like 180, 360,720 ... degrees  in our pricetime Universe. Plus harmonic waves may bring some important information regarding the price movement as well.

Technology

We can describe the whole technology by three steps:

Step #1: Choose important turning points Let it be our turning points: bottom Mach 6, 2009 - to April 26, 2010.

Step #2:  Draw "2D Time-Price planetary distance/equidistant circles"  charting tool through these important turning points:

and try different planetary combinations there:

I recommend to start with:

 Sun (Sun-Sun combination) - pricetime Annual circles;

Sun-Mercury helio  - pricetime Mercury synodic circles;

Sun-Venus helio  - pricetime Venus synodic circles;

Sun-Mars helio  - pricetime Mars synodic circles.

Actually you can try any planetary combinations. For example, Sun-Mars geo circles look very interesting.

Step #3: scaling these circles and watch how these circles hit important turning points.

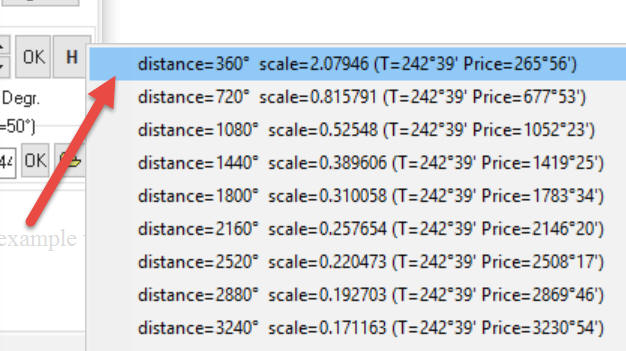
Click "H" button, and the program will show you the list of scaling coefficients that provide "good" distances between our turning points:

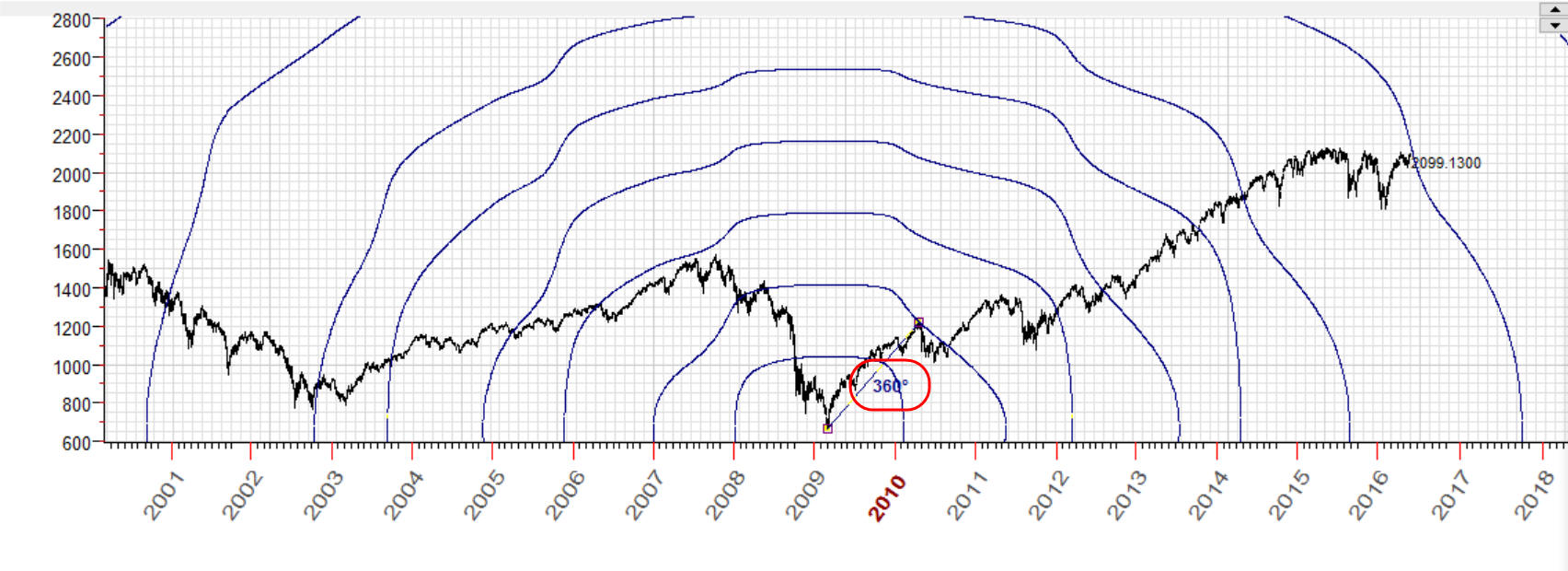
As an example I have selected Sun-Mars geo planetary combination as time metrics. Highlighting the first item, we set the scaling coefficient to 2.07946. The pricetime distance between our turning points will be 360 degrees:

and I got these equidistant circles:

This video explains how to do that:

IMHO, these figures should work as Fibonacci ellipses charting tools, so I do not dig into details here.  The advantage of this approach is that it provides the formal procedure: choose two turning points, check about a dozen of planetary combinations, and for each planetary combination we have 1-3 scales that provide "good" distances between chosen turning points.  There are a few dozens (usually a dozen) variants that may be easily estimated from a trader's point of view.

Interference

If we accept that these cycles represent a kind of information waves in pricetime Universe, we are expecting to see interference between these waves. This video explains how to do that: