The Tidal Force
Gravitational Force
Ask yourself what force you feel every second of you life. This is a gravitational force between your body and the Earth, or in other words, your weight. If you manage to put your body on Jupiter's surface (though the physical conditions there make this experiment impossible), your weight will be twice more. This is because Jupiter is a very massive planet, and its gravitational force is much more stronger. From the other side, if you make a travel to the Moon and have a walk enjoying the Moon's landscape, you will see that your weight is 6 times less (instead of going there, watch the famous movie about the first walk on the Moon by American's astronauts in the year 1969; they are practically flying).
The gravitational force discovered by Sir Isaac Newton in the year 1687 is the most enigmatic force. The modern science considers the gravitational force as the result of space-time curvature: simply any body modifies the topology of the space around, and this fact causes the attraction between two bodies . In the two-dimensional Universe, this space curvature looks like this (this picture is from the website www.wikipedia.com), I think this is obvious why all bodies move toward the Earth in the two-dimensional universe:

To figure out how it goes in our three dimensional Universe, we need to see this picture in four dimensional space; this is very difficult.
Now let's go back to our Earth problems. Sitting in a coffee shop (like I do now), you experience not only your weight (as the attraction between you and the Earth), you also always experience the attraction of the Sun (which is 4500 less than the Earth's), the Moon's attraction (800,000 times less), and the attraction of other planets as well (though it is extremely small).
Here is the table of the average gravitational force for all planets assuming that gravitational force of the Sun is equal to 1:
| Earth | 4500 |
| Sun | 1 |
| Moon | 0.0055 |
| Mercury | 0.000,000,15 |
| Venus | 0.000,0019 |
| Mars | 0.000,000,11 |
| Jupiter | 0.000,034 |
| Saturn | 0.000,0031 |
| Uranus | 0.000,000.11 |
| Neptune | 0.000,000,057 |
| Pluto | 0.000,000,000,22 |
As you see, the Sun's gravitational force dominates here while the effect of other planets is non-significant. If we exclude the Sun and keep analyzing the gravitational force of all planets, the Moon will dominate.
Tidal Force
The tidal force is much more interesting. Let's first find out what is that.
Imagine that you are a scientist and you need to conduct this experiment: sitting in your office try to measure how the Moon attracts your pen. I mean here the gravity, the gravitational attraction. Your office is located on the 18th floor. Then do the same experiment in the lobby. Compare the results; you may find that these forces are different. Why is it so? Because the distance to the Moon from your office and from the lobby is different. True this difference is very small; however it produces a huge impact on the Earth.
The most known effect of this force is the rise and fall of the sea level with respect to the land. This is why this gravitational force of the Moon has a special name of "the tidal force".
This effect is not a privilege of the Moon only. Any body in the Universe has it. And it is different for different bodies. It can have a really huge impact. As an example, the tidal force of the Black Hole is tremendous. If your pen would be put not far from the Black Hole, the difference between the gravitational force that affects two sides of your pen is so huge that it simply destroys the pen. The tidal force around the Black Hole destroys all bodies, only atoms can exist there.
The table below represents the tidal forces of the Sun, the Moon, and the planets. Again, the Sun's tidal force is considered as 1, and the other tidal forces are compared to it:
| Sun | 1 |
| Moon | 2.14 |
| Mercury | 0.000,000,15 |
| Venus | 0.000,0017 |
| Mars | 0.000,000,066 |
| Jupiter | 0.000,066 |
| Saturn | 0.000,000,33 |
| Uranus | 0.000,000.0062 |
| Neptune | 0.000,000,0019 |
| Pluto | 0.000,000,000,0061 |
So you can see that the effect of the Moon dominates here - because it is the closest body to the Earth. Though the effect of the Sun is strong enough, it is twice lesser than the Moon's. The effect of other planets is very small.
There is a hypothesis that tidal forces (of the Moon and other bodies) affect the stock market. Remember that this is just an idea; no mechanics of the process is yet described and proven. Timing Solution is able to calculate these forces. How to do that?
For your convenience, if you work with the intraday data, you can calculate diurnal tidal forces through ULE module. You can find this item in the standard events library:
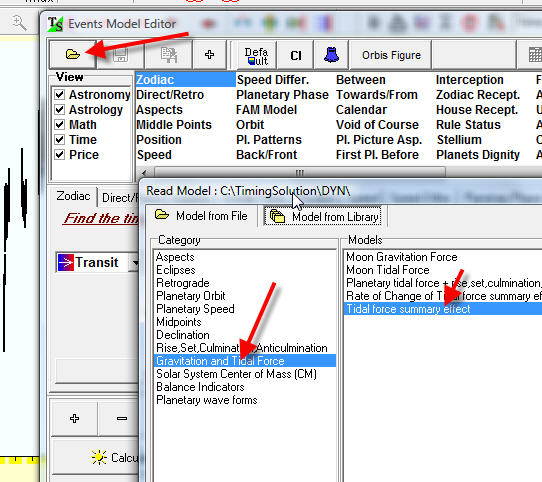
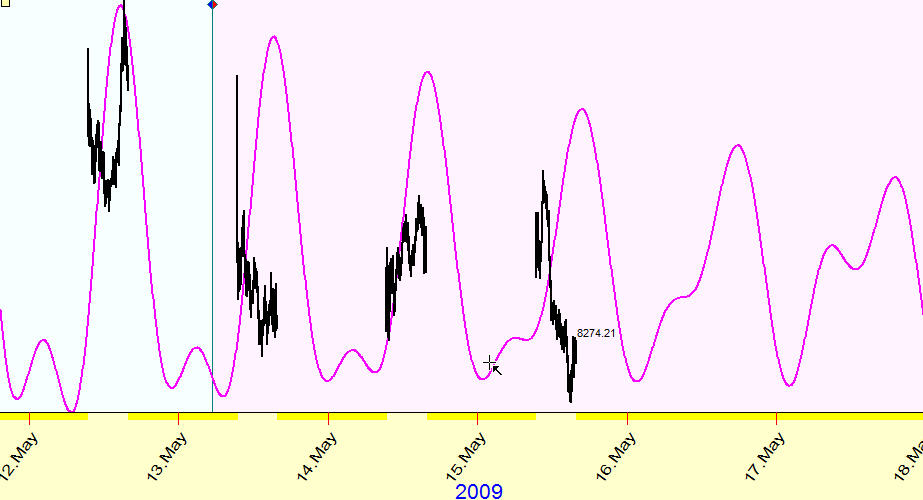
This is how it looks together with the intraday Dow data:
here is the bigger scale:
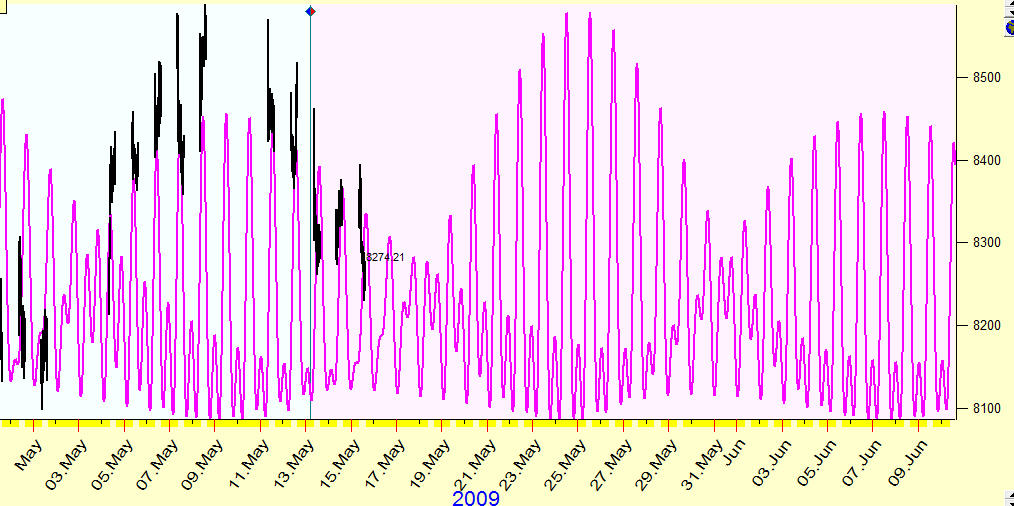
The most influence is caused by the Moon's and the Sun's tidal force; the effect of other planets is practically zero.
Also pay attention that the maximum of the tidal force's effect correspond to the Moon's culminations and anti culminations:
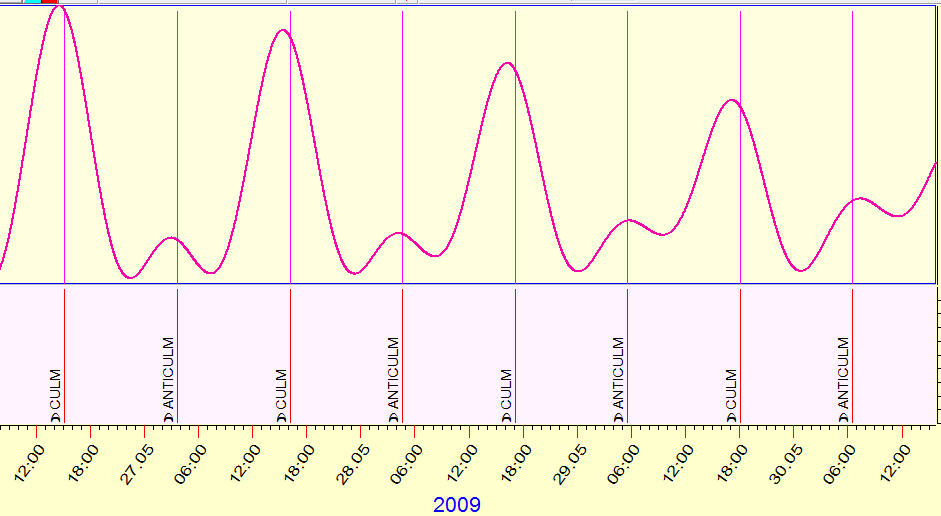
Resultant Tidal (RT)
There is one more interesting question there - the direction of the tidal force, i.e. the Zodiac zone the resulting tidal force of all planets points at. We know that the force of the Sun and the Moon dominates here, so the the resultant tidal is expected to be located between the Sun and the Moon, closer to the Moon. At the New Moon and the Full Moon it coincides with the Moon's position.
Let's call this point Resultant Tidal - RT. To calculate RT, you can create an additional object ("Options"->"Customize Objects") this way:
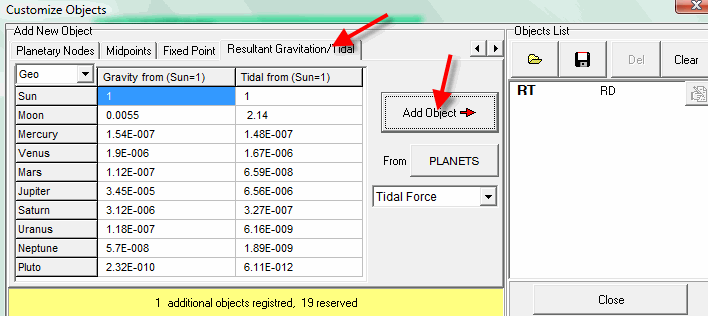
and use this point everywhere in the program.
Here are 8 subsequent diagrams that show how the resultant tidal moves in respect to the Sun and the Moon (the interval is two days):
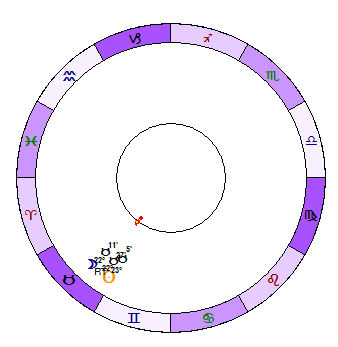
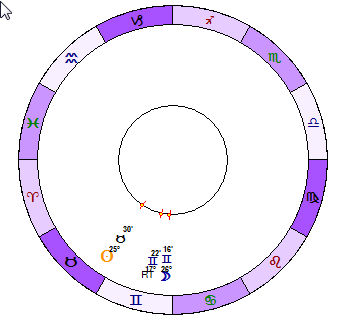
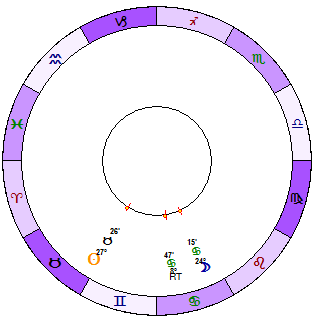
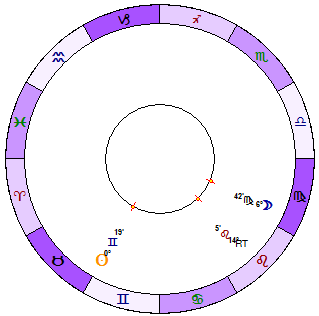
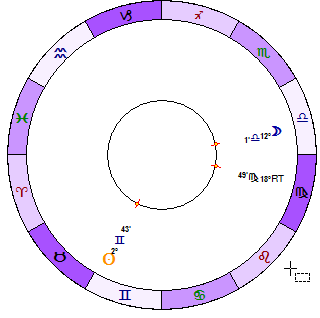
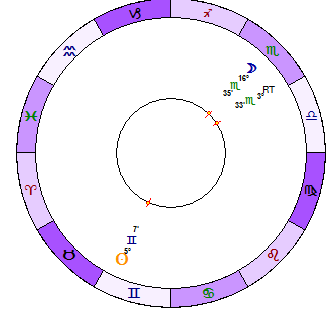
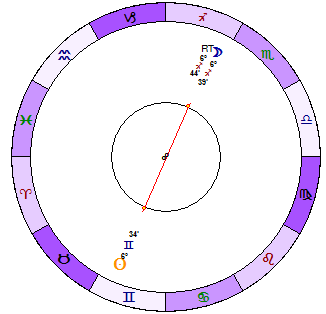
or look how Resultant Tidal moves in respect to the Moon (blue - the Moon, green - Resultant Tidal):
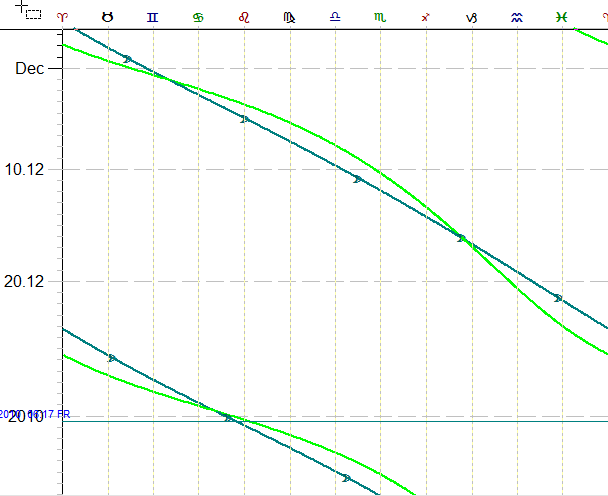
This very interesting phenomenon that we got is a kind of synodic cycle. Compare it to how Mercury moves around the Sun:
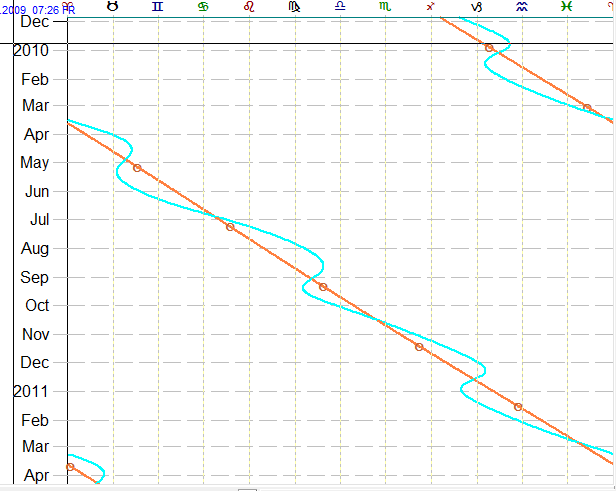
Mercury moves around the Sun, the maximum angle separation varies between 18 and 28 degrees. The moments when this separation reaches its maximum are called ELONGATIONS, and there are two types of the elongation - Eastern and Western.
Exactly the same way we can define New Moon/Full Moon elongation for Resultant Tidal as a maximum angle separation between Resultant Tide and the Moon. See it here:
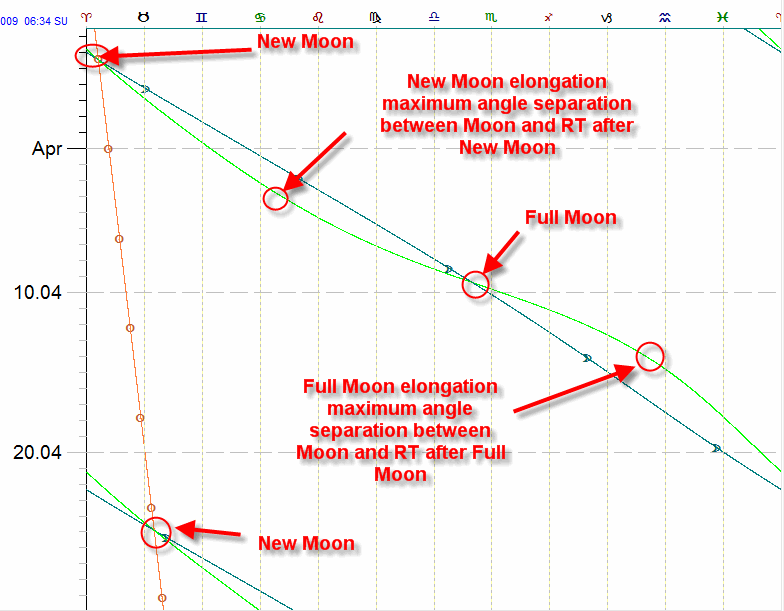
Usually the elongation varies in the range of 25-35 degrees, look how this angle changes in time:
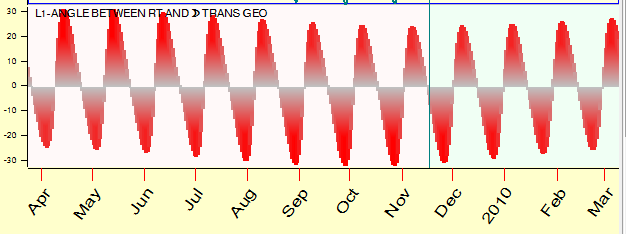
or in a bigger scale
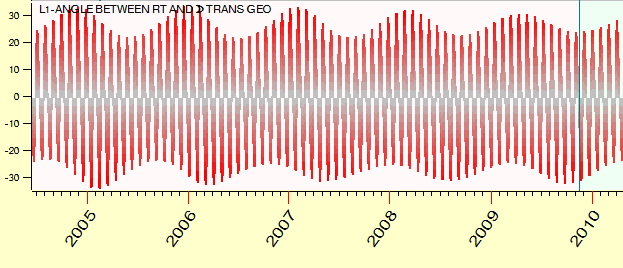
The elongation points have an impact on the stock market. I will show how to conduct this analysis.
Start with the Composite curve for the angle separation between Resultant Tidal and the Moon calculated for Dow Jones Industrial Index since the year 1885 till November 2009:
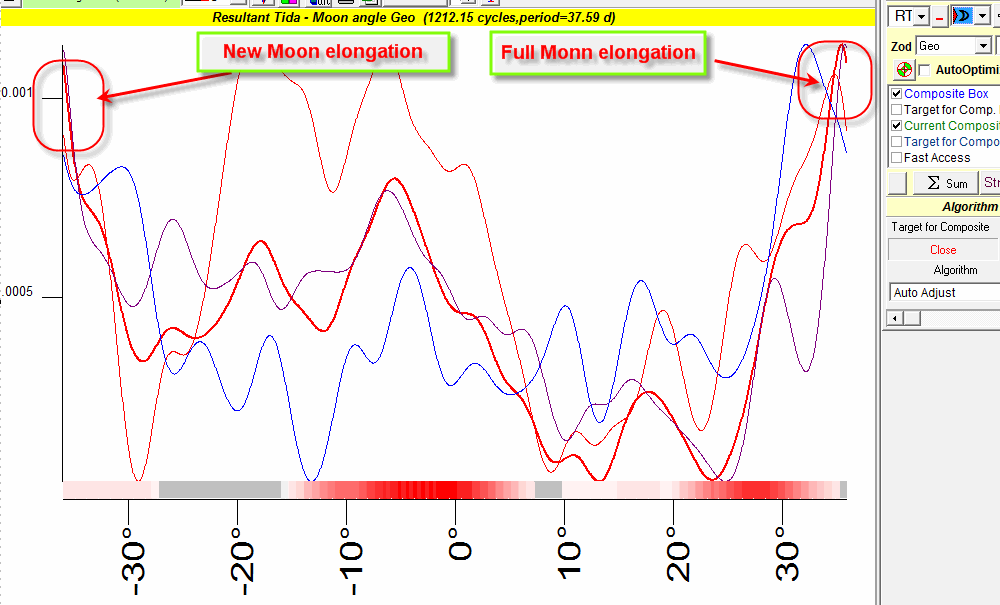
As you can see the price is higher in Tidal Direction elongations.
Thus we can state this rule:
The price is higher when the angle separation between Resultant Tidal and the Moon reaches its maximum (i.e. elongation points), especially after the Full Moon.
You can calculate New Moon elongation for Tidal direction through ULE module this way:
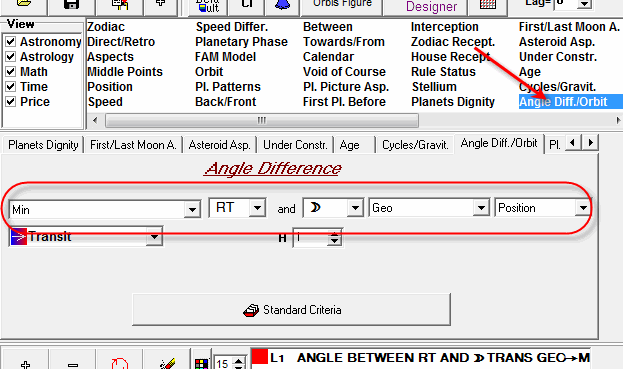
This is how the New Moon elongation points for Tidal Force have worked for the last several months:
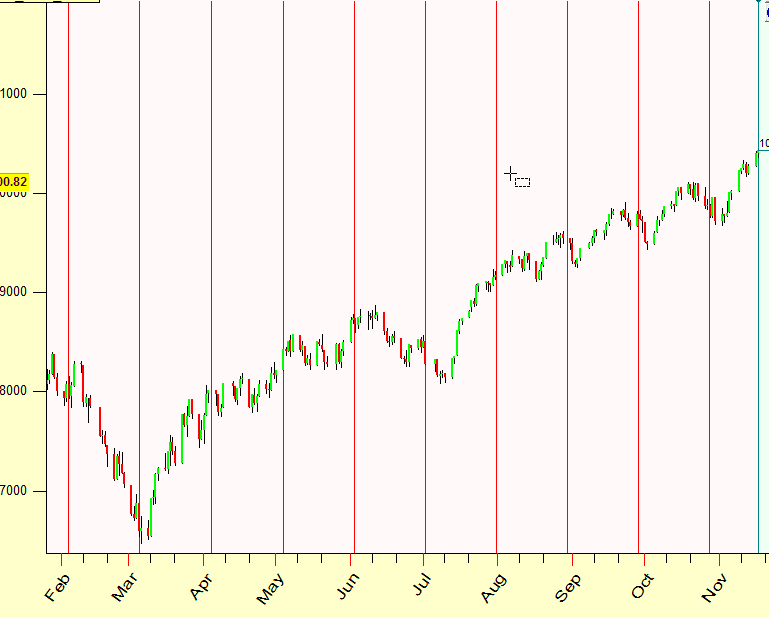
For Full Moon elongation for Tidal direction set these parameter:
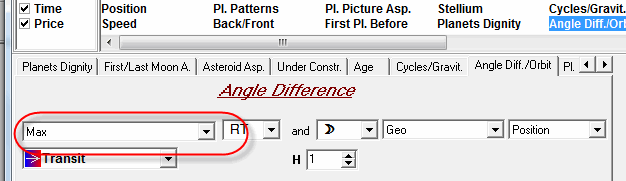
This is how this phenomena worked:
Heliocentric Tidal Force Direction
This is the force that affects the surface of the Sun by other planets of Solar System. Two planets are dominate here: Venus and Jupiter, so the position of heliocentric Resultant Tidal is always located between Venus and Jupiter. Look how the planetary line for heliocentric RT looks:
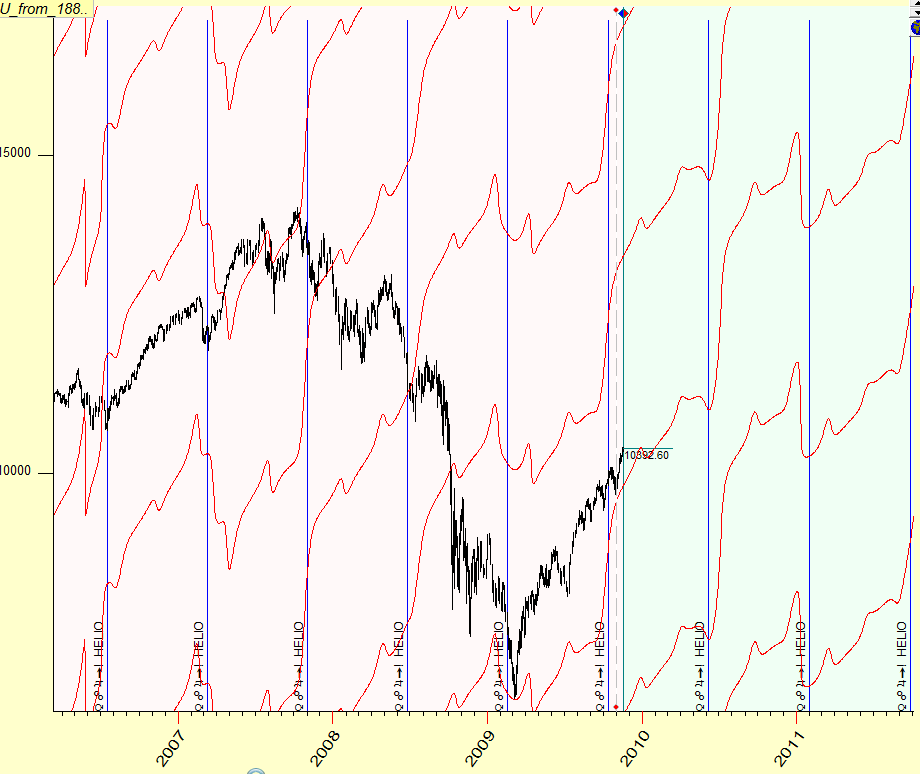
Pay attention that this planetary lines moves irregularly when heliocentric Venus makes opposition aspect to Jupiter.
This subject needs additional research.
November 17, 2009
Toronto, Ontario