What is the Correlation Coefficient?
This is the definition from Financial Forecast Center (http://www.neatideas.com/cc.htm).
What is the Correlation
Coefficient?
The correlation coefficient
concept from statistics is a measure of how well trends in the
predicted values follow trends in the actual values in the past. It is a
measure of how well the predicted values from a forecast model "fit"
with the real-life data.
The correlation coefficient
is a number between 0 and 1. If there is no relationship between the
predicted values and the actual values the correlation coefficient is 0 or very
low (the predicted values are no better than random numbers). As the
strength of the relationship between the predicted values and actual values
increases so does the correlation coefficient. A perfect fit gives a
coefficient of 1.0. Thus the higher the correlation coefficient the
better.
The correlation coefficient varies in the range of -1 (-100%)..+1(+100%). Timing Solution software measures the correlation coefficient in %%. It means that instead of r=0.123 we use r=12.3%
Practice shows that for financial analysis it is better to use percentage. For example, suppose we have found the projection line that provides correlation 5%. Following the usual notation, it should be marked as r=0.05.
It can be easily misread as r=0.005, especially when you analyze many correlations (like in Walk Forward Analysis reports).
If you use percentage notation, it is r=5% versus r=0.5%, you never mix them up. It is a convenient way as 5% level is very important (see below the explanation).
What correlation is good enough? The more the better. Usually, the models that we analyze provide 10%-20% correlation. Sometimes it is more than that, but these results are not stable. To be sure that the result is not accidental, it is necessary to have a sufficient amount of price bars for calculating the correlation. For practical usage, you can use this table:
| Correlation | Meaning |
| 100% | means ideal coincidence between some data and the projection line |
| 5% | weak correlation, this projection line is not usable though it reflects some stock market movements |
| 10% | we can take it as a not bad correlation |
| 15% | good correlation |
| 0% | no correlation. Two sets of data are not related |
| -100% | this is anti-correlation, which means that the predicted values "mirror" the actual values (or one data set is the "mirror" for another one). |
These are examples:
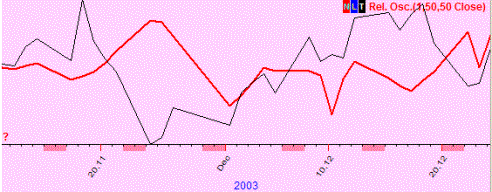
Positive correlation (50%); these two curved lines show the same price movement (most of the time). In other words, a predicted price and the actual one show the same price movement (up or down):

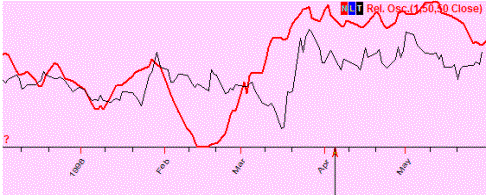
No correlation (7%); these two curved lines show totally different movements (if one goes up, the other may go up or down and there is no regularity seen there):
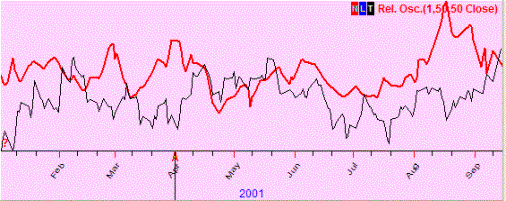
Negative correlation (-4%); we observe the "mirror" effect (when one curved line goes up, the other one goes down in most cases, and vice versa):