Heliocentric declination - astrology without astronomy
Very often I receive the question "How to calculate HELIOCENTRIC DECLINATION for some planets?�. And I always have to provide the same answer: "My friends, there is no such a thing in Nature as Venus heliocentric declination (as an example)".
This misunderstanding came from George Bayer�s book "Stock & Commodity Trader's Hand-Book of Trend Determination". Please check any of his rules where "heliocentric declination" is used. Let us look together at the Rule N30 and check it using the ephemeris. You will see easily that Bayer speaks about regular declination in geocentric coordinates.
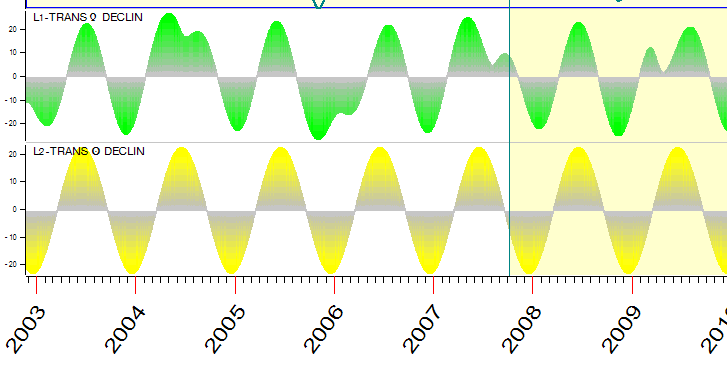
Declination is the latitude of the planet in Equator coordinates (accordingly, Right Ascension is the longitude). Usually it changes between 23-rd South and 23-rd North degrees; sometimes the planets exceed these borders (especially Pluto though it is not a planet any more).
I put here declination diagrams for the Sun (yellow) and Venus (lime):

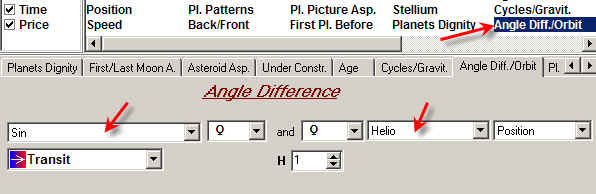
I know the only way to calculate "heliocentric declination". You may follow these steps:
a) calculate heliocentric longitude for any planet;
b) find what declination of the Sun corresponds to this longitude (now we assume geocentric longitude).
You can easily calculate this declination as Sinus of heliocentric longitude:
But you always should remember that:
1) this "declination" has not any connection with the astronomical reality;
2) George Bayer did not use it.
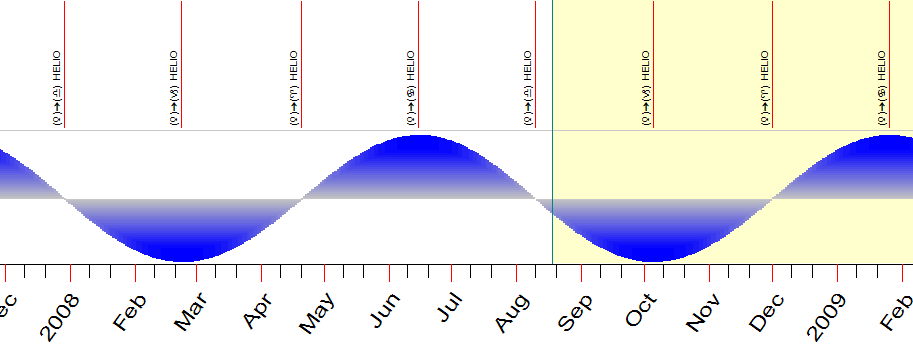
The important points of this "declination" Zodiac correspond to Venus�s ingress to cardinal signs in heliocentric coordinates (Aries changes the semisphere from South to North, Cancer - max north declination, etc):
I believe this is a simple mistyping in a book that continues to live.
Somehow this situation reminds me one ancient Hindu legend: "One old master of yoga used to tie his cat to the nearest tree when he did a prayer. It was his favourite cat, and it bothered him constantly, so the master had no other choice. Times came by, the master passed away, and his followers continued the work of their teacher. Before starting a prayer, they looked for a cat, and it became a mandatory part of the praying ritual. They would not pray until some cat was found and tied to the same tree."
I understand the respect that we all have to the great masters of the past. However, in my opinion, they would be more pleased if we understood what they actually were doing�
To finalize this subject, I would like to explain how the heliocentric declination should be calculated from astronomical point of view.
The first thing we need to know is to calculate the true Solar Equator. I mean a not well known Solar Equator that represents Earth's rotation but the Sun's rotation. This true Solar equator is inclined to Ecliptic at the angle of 7 degrees 15 minutes (obliquity to Ecliptic). It means that the heliocentric declination will be always less that 23 degrees (except Pluto). For most planets the heliocentric declination varies mostly in a range of -10 - +10 degrees (obliquity to Ecliptic plus heliocentric latitude).
Here is the table of maximum values for the heliocentric declination:
| Mercury | 14 degrees |
| Venus | 11 degrees |
| Earth | 7 degrees |
| Mars | 9 degrees |
| Jupiter | 9 degrees |
| Saturn | 10 degrees |
| Uranus | 8 degrees |
| Neptune | 9 degrees |
| Pluto | 25 degrees |
I tried to find some info regarding the true Solar Equator, but could not find it. Maybe it is very hard to measure it precisely, because the Sun is not a solid body. See the explanation below (from http://www.wikipedia.com):
"As the Sun consists of a plasma and is not solid, it rotates faster at its equator than at its poles" and "The period of this actual rotation is approximately 25.6 days at the equator and 33.5 days at the poles. However, due to our constantly changing vantage point from the Earth as it orbits the Sun, the apparent rotation of the star at its equator is about 28 days.[25]"
Another reason is the fact that the usage of Solar Equatorial Coordinates (i.e. coordinates that are derived from Solar rotation, i.e. true Solar Equator) has no practical sense, at least so far. These coordinates can be used only for mapping celestial bodies observed FROM THE SUN. So far this is not an actual task for obvious reasons.
'