Upgrade June 18, 2005

Detrended Zigzag

This patch allows to create the detrended zigzag. The detrending procedure applied to zigzag method allows to calculate the Spectrum and Composite for it as well as to use this zigzag in the Neural Net module. Thus, now we are able to reveal any kind of periodicity that might exist in the time distribution of turning points.

Generally speaking, zigzag is the line that we draw while connecting together tops and bottoms of the price line. Another name for zigzag is "filtered waves" (this theory was created by Arthur A. Merrill). The biggest problem with zigzag is that we cannot use it for big time intervals due to the existence of market trend. But - what if we try to eliminate the trend? Thus, we get the detrended zigzag. (By the way, it is a good example of mutual cooperation with the users of Timing Solution. This idea was born in our discussions of the subject.)

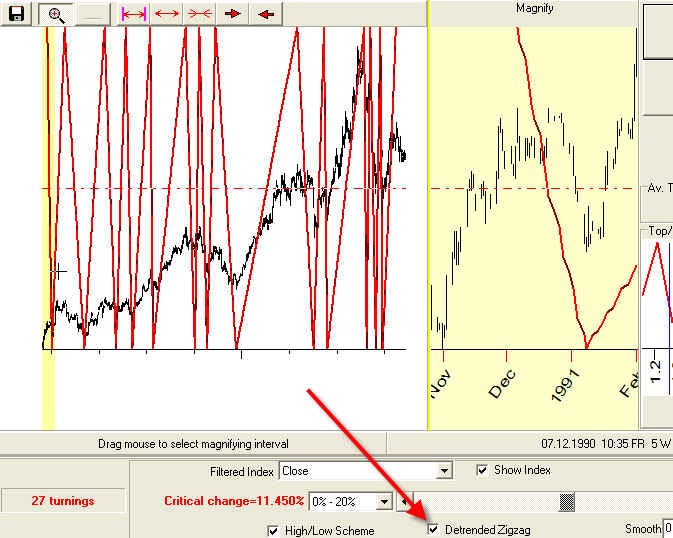
You can define the detrended zigzag here:

To see the difference between the regular and detrended zigzag, let's draw them both on the same screen:

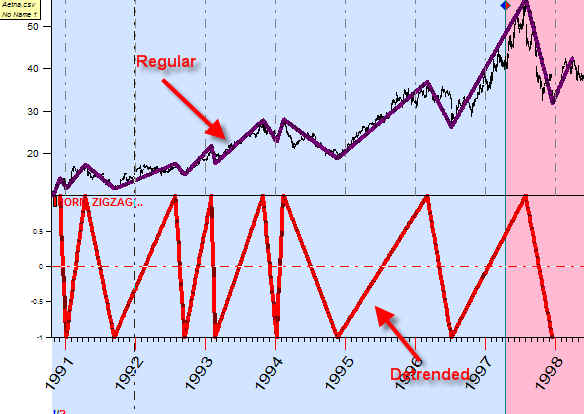
The usage of the detrended zigzag makes possible the analysis of turning points for big time intervals (due to elimination of the trend).

While the detrended zigzag is created, we can use it in all modules of the program. For example, we can calculate Spectrum for it. It will give us the time periods with high probability of turning points:

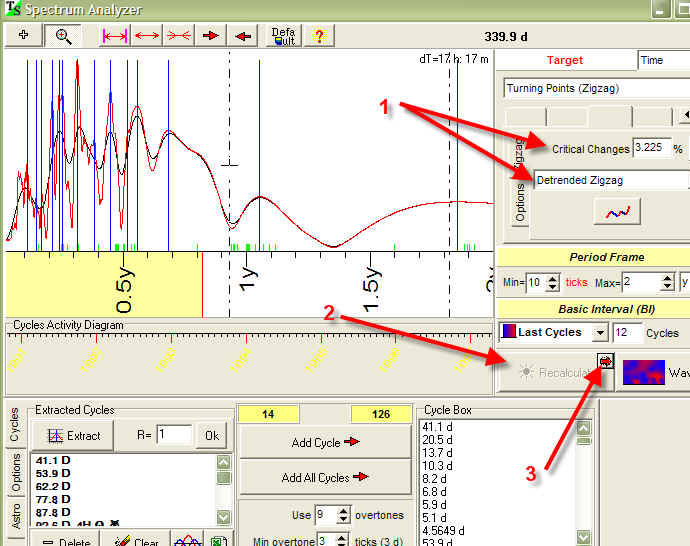
Remember that the program does many operations automatically.  You have to define only crucial points of the process; simply follow the steps shown on the picture above. 

Extract the most active cycles. The program puts these cycles into the clipboard automatically.

When it is done, we can create the  Neural Net model and predict the future turning points. How do we do that?

First of all, define outputs (i.e., things that we want to predict). In our case, this is the detrended zigzag with critical change 3.225:

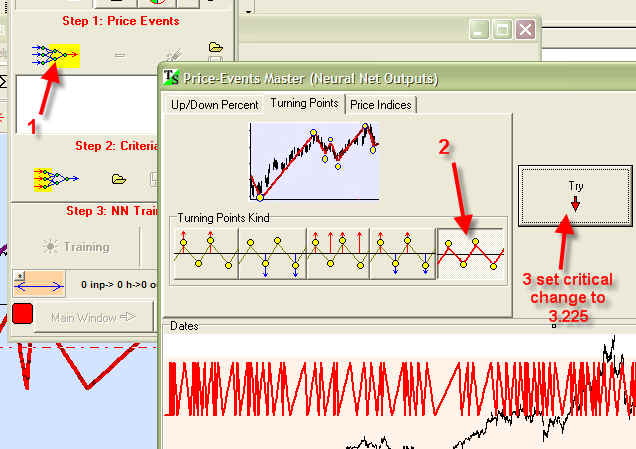
Next step is to define inputs, or factors that we use for prediction.  In our case, we use regular cycles calculated by Spectrum module. These cycles are already found, we get them from the clipboard:

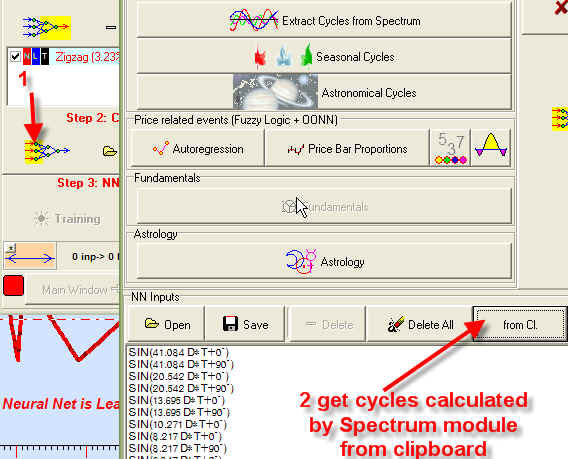
The next step is to train this model. 

This simple technique provides surprising results. See the picture below; it shows how well: this model allows to predict the turning points, although sometimes we still face the "inversion" effect: 

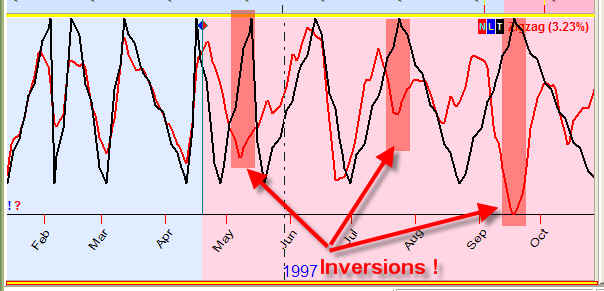
At the inversions, the model replaces tops and bottoms. But the most important fact is that this model points out the correct time when the turning point occurs no matter what its nature is (in other words, no matter whether it is a top turning point or a bottom one). 

Also, due to its whole appearance as teeth of the saw, the detrended zigzag is able to locate turning points more precisely than with any existing oscillator.

All the above gives us a very strong reason to use the detrended zigzag for creating timing models.

June 18, 2005

Sergey Tarassov

Toronto, Canada