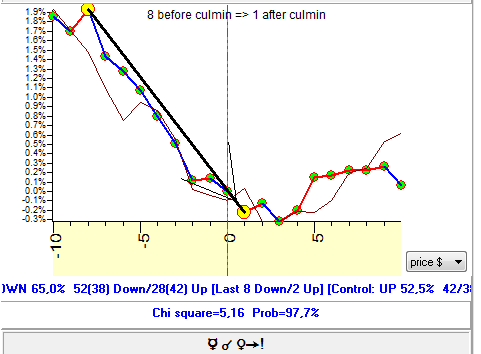
Chi Square Criterion in efficiency test module
This class is the answer to a question received from some Timing Solution user:
I am not sure to understand the meaning of the probability figure
appearing in the efficiency test when the Chi-square appears.
In the enclosed example, what is the probability of a down move? Is it 65% or
97,7% ?

In brief, the probability of the downtrend here is 65%. In other words, you expect that this financial instrument's price will drop, so you open a short position 8 days before the culmination and close it a day after the culmination, - you may win 65% of trades. I.e. in 65% of cases the price will drop. The rate of winning trades here is 65%.
Next step is: we need to understand wether it is an occasional/random fact (just another trick of Chaos) or it is a statistically significant and trustworthy fact. In order to understand that we create a control group. How do we do that? We make randomly 80 short trades: open a short position and close it in 9 trading days. We do it focusing on 9 trading days in a row, and the opening date is random, not considering the date of the culmination. And this is what we get:
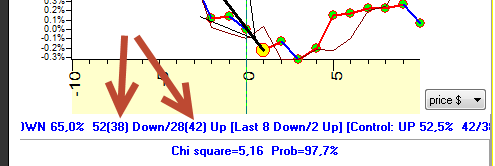
Price went down 38 times versus 42 time up i.e we have 47% winning short trades; the amount of losing trades is more than the amount of winning trades.
Once again:
if we adjust our short trades to the culmination of the aspect (or other phenomena), we get 65% of winning trades,
while
if we make similar trades randomly, we get only 47% of winning trades.
Next step is to understand: is this difference between 65% and 47% big enough or not so big? The chi square criterion is developed for that. In this case it tells us that, with the probability 97.7%, it is not an accidental fact. We receive 65% due to the effect of this aspect's culmination, it is how this culmination works for our financial instrument. Ignoring this culmination, we will not be able to get these 65% of winning trades if we trade randomly; this is true with the probability 97.7%. Do not confuse these percentages. 65% is the amount of winning trades in regards to the aspect's culmination, while 97.7% says that we can rely on that info while planning our trades.
And here is one subtle though very important nuance. All calculations discussed above were made according to regular statistics, based on a normal distribution of data - exactly how I was taught in my University. In reality, the normal distribution does not work for financial markets. Just does not work. And - as of now, it is not agreed yet what math rules work better. It is a problem of fat tails in statistics; google it, you will find yourselves. I have wrote some related notes here: http://www.timingsolution.com/TS/Articles/cds/index.htm
In reality, it means that for our case, the chi square is much less, significantly less. It means that random, unexpected surprises have more chances that it is allowed by standard math statistics.
Personally, I used to use 1/3 of the chi square value. So, in our case chi square is 5.16. Divide that by 3. We have 1.72. and the probability is 81%. Yes, it is less than the previous 97.7%. However, it is something that I can really rely on. Another variant, you can also use standard chi square calculator but use 2-3 degrees of freedom.
See below the table that allows to calculate 1/3 chi square criteria. It works this way, look at chi square value, it is here in our case 5.16:
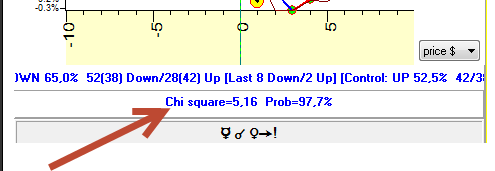
according to this table the nearest to 5.16 is 5 so 1/3 chi square criteria indicates 80% confident level:
| Chi square value | Probability standard formula |
Prabability 1/3 chi square |
Probability degrees of freedom=3 |
| 2 | 84% | 59% | 43% |
| 3 | 92% | 68% | 61% |
| 4 | 96% | 75% | 74% |
| 5 | 98% | 80% | 83% |
| 6 | 99% | 84% | 89% |
| 7 | 99.2% | 87% | 93% |
| 8 | 99.5% | 90% | 95% |
| 9 | 99.7% | 92% | 97% |
| 10 | 99.8% | 93% | 98% |