Anti-Information

written by Sergey Tarasov November 23, 2016

Anti-Information versus Zero-Information

This article is about inversions. It looks like within last several months, step by step, I am starting to understand how to work with them.

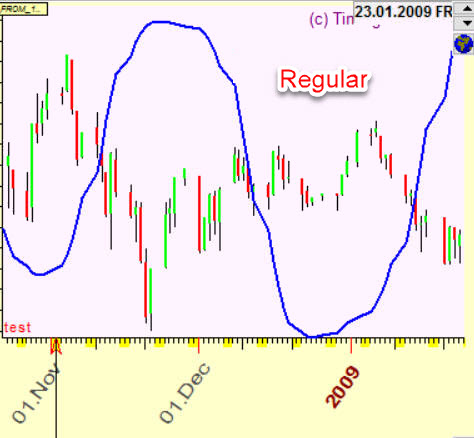
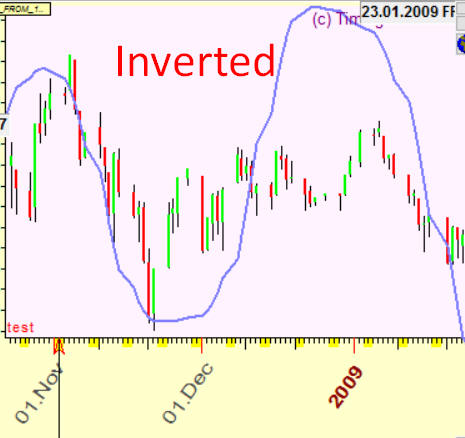
Before any discussion and following a good old mathematical tradition, let us start with a definition what an invertion is. This is a situation when an inverted/flipped projection line provides us a better forecasting result than a regular projection line. This is an example:

So, we can define an inversion this way: it is a situation when our forecast follows the opposite way. This is a kind of inverted reality, like as on this picture that I made at my favorite Kettle Lake:

You see there real trees with real leaves, and you see the same trees and leaves reflected in the water. I tend to think that sometimes this reflected reality works as well as the original reality. And it looks like some of mathematical apparatus that deals with this reflected reality has been found as well.

Traders know the inversion phenomenon very well. It happens from time to time: we may calculate a projection line to predict the future or apply some indicator, and in reality the price action is totally opposite. It is not totally wrong but inverted. To get the correct forecast, we need just to invert the projection line.

Now is the time to enter the word that is the theme of this article: anti-information.  This is not a zero information or absence of any information. Zero information is a kind of white noise in statistics. This is a situation when a model is able to forecast some times and some times it is not, and we do not know when these switches take place. The probabilities to get correct and not correct forecasts are equal, so we cannot make any decisions based on this info. This is Buridan's ass paradox when that beast is equally hungry and thirsty and has to die because it cannot make any decision. Anti-information is a different entity, this is a situation when the projection line works inverted way for a significant period of time. It means that this is the information that can be used positively to forecast the stock market or something else.

A good example of using a negative information is a contrarian investment or bid. Or take a recent example from politics: Donald Trump's victory while the most of analytics have forecasted Hilary Clinton's victory.

My major point is: this situation with inversions/negative information is not a mistake only or some breath of Chaos. This is a mathematical entity, an information with minus sign. This is not a bad information, and it can be used as a regular information. Going back to my picture above, we can gather the information that the fall is coming just watching the reflection of those trees in the lake.

If we accept the fact that the information may be with minus sign, many things will be possible in financial mathematics. For example, when I wrote a code for Walk Forward Analysis module to estimate the workability of different models, I simply ignored inverted projection lines taking inversions as a mistake or some tricky game of Chaos. From some moment, I have recognized that this way I see only a half of the whole picture. This thing is pretty much the same as an invention of negative numbers 26 centuries ago: accepting the fact that there are digits lesser than zero, we have obtained an ability to solve mathematical problems that were unsolvable before that.

In other words, we have a dilemma on how to handle inversions. In my practice, this dilemma appears this way: to analyze the forecast ability of our model, we apply Walk Forward Efficiency (WFE) value. As an example, let say WFE is 80%. It means that in 80% of all considered cases, the projection line provides a good forecast, while for 20% it does not forecast. It is so, if there are no invertions. The dilemma appears when our model provides inverted projection lines. So, in 80% cases, though our model has provided an inverted projection line, it still forecasts the future, only the projection line should be inverted. If we assume that this is just some game of Chaos, we must set WFE for this model to zero (which means that there is no positive/useful information). If we assume that this information is useful, we can set WFE to minus 80%. What approach is more proper? For the last ten years, I have applied the first approach: now I am not that sure...

How it works

The last mile stone to convince me in accepting this idea was Q Spectrum module: http://www.timingsolution.com/TI/16/index.htm

Firstly I simply ignored inverted cycles taking them as Chaos game. But I could not ignore the fact that, beside regular cycles, Q-Spectrum module also indicates the activity of inverted cycles. This is how it looks:

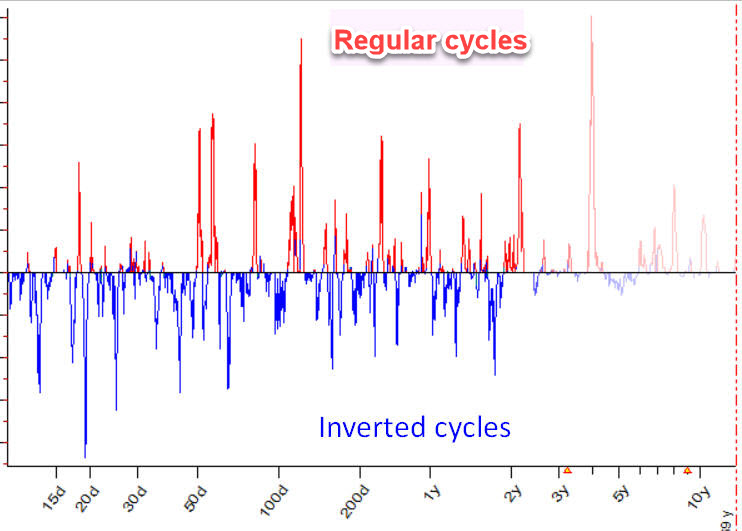
This activity does not look as a common white noise: exactly like there are regular classical cycles (red peaks on the chart above), there are peaks for inverted cycles (blue peaks). We cannot ignore the existence of inverted cycles; otherwise we should ignore regular cycles as well.

Pay attention to this: the classical spectrum (Fourier transform) does not "see" inverted cycles. And look at the chart below where Q-spectrum results are shown together with classical spectrum (green):

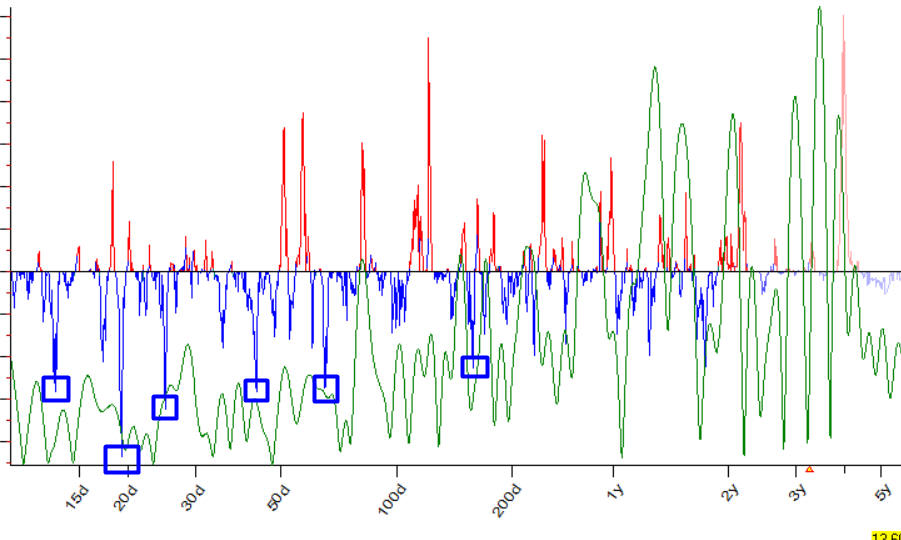
From the point of view of classical spectrum, inverted cycles do not exist, no activity there, therefore nothing exist there.  But - these cycles do exist! To see them, we have to conduct Walk Forward Analysis, and this is what Q Spectrum does.

How did I know that these cycles existed? The answer is Annual cycle; it was an enigma for me. Classical spectrum does not see Annual cycle at all while I know for sure that Annual cycle works. I did not understand what is wrong there and was looking for the error in my code. When I ran Q-Spectrum module for EOD SNP500 for the first time, I immediately have recognized that everything is in the right place now. Annual cycle have been found by Q-Spectrum with very high accuracy - 364.4 days versus 365.2. And there is  380.6 inverted cycle nearby:

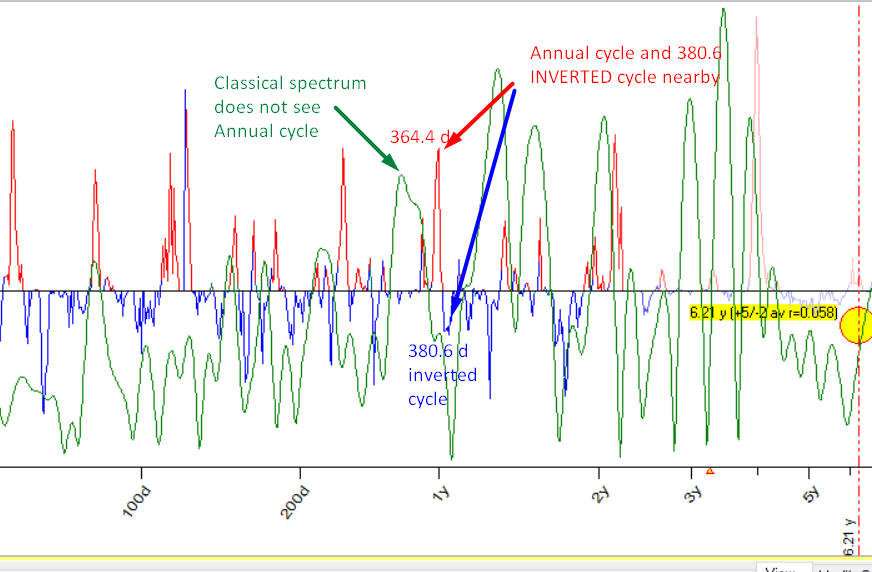
Maybe this is the reason while classical spectrum ignores these cycles: from the point of view of classical spectrum, these cycles interact each other, and this fact mixes the whole picture.

This was the first evidence for me that I am on the right way.

The second evidence came several months later as back feed from Timing Solution users. This is an important factor too.

Pro et Contra

All "pro" arguments have been explained above, now let us discuss "contra" arguments. I personally do not like inverted cycles and prefer to avoid them. Definitely we cannot consider regular and inverted cycles as equal. It is like reflected trees of Kettle Lake cannot be considered the same as common trees that grow from the earth. The life of the inverted cycle is different than that of a regular cycle. Suppose that today, on November 23, 2016, we have found that 100-days cycle starts working as an inverted one, while before it worked as a regular cycle. So, starting from today, we have to invert our projection line to get a better future forecast. After some time (100 days? maybe 200 days? who knows...) this projection line may become a regular one, and starting from that moment we have to invert it once again. Regular cycles work in the same manner all the time while inverted should be inverted from time to time. This is a different mathematical entity, and actually I do not quite understand what to do with it. The inverted cycle is a cycle with a secret, and we always should be alert for the next inversion date. I do not know what is the price for this uncertainty, this is my main "contra".

Accepting the negative information (inverted cycles), we automatically shake our World, things in it becoming less certain. However, we have a branch of knowledge - theoretical physics - that lives in such World for a hundred years already; in quantum physics nothing is certain. As Stephen Hawking said, "nothing certain in quantum World, even our existence...".  At least, using inverted cycles we can more precisely calculate a very certain Annual cycle; this is "pro".

For your information, here are my previous articles regarding inversions:

http://www.timingsolution.com/TS/Mini/46/index.htm

http://www.timingsolution.com/TS/Mini/113/index.htm

November 23, 2016

Toronto, Canada